(Solved): Determine the differential equation of motion for the damped vibratory system shown by solving for ...

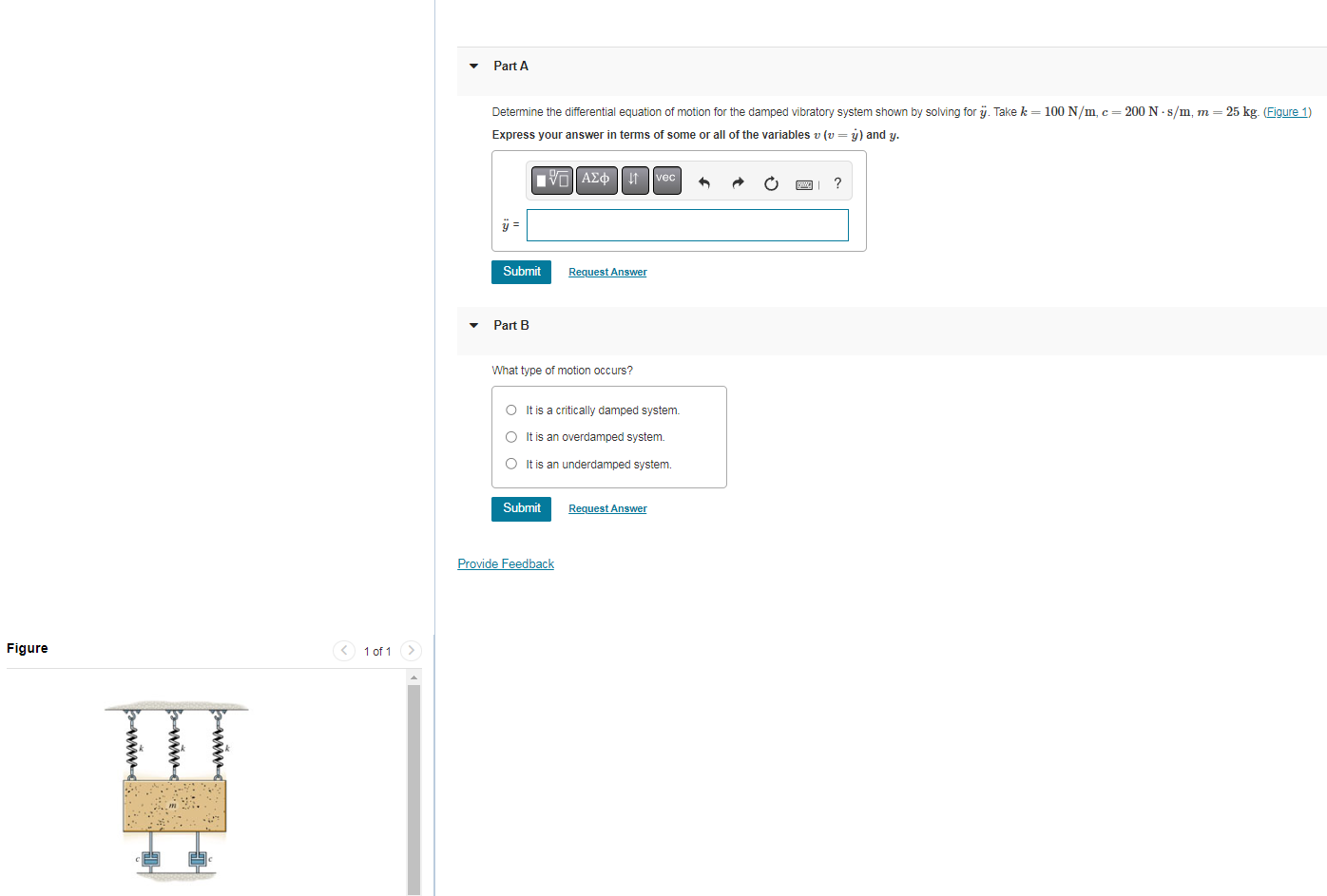
Determine the differential equation of motion for the damped vibratory system shown by solving for \( \ddot{y} \). Take \( k=100 \mathrm{~N} / \mathrm{m}, c=200 \mathrm{~N} \cdot \mathrm{s} / \mathrm{m}, m=25 \mathrm{~kg} \). (Figure 1) Express your answer in terms of some or all of the variables \( v(v=\dot{y}) \) and \( y \). Part B What type of motion occurs? It is a critically damped system. It is an overdamped system. It is an underdamped system.