(Solved): Determine the carburizing time (in s) necessary to achieve a carbon concentration of \( 0.44 \) wt ...

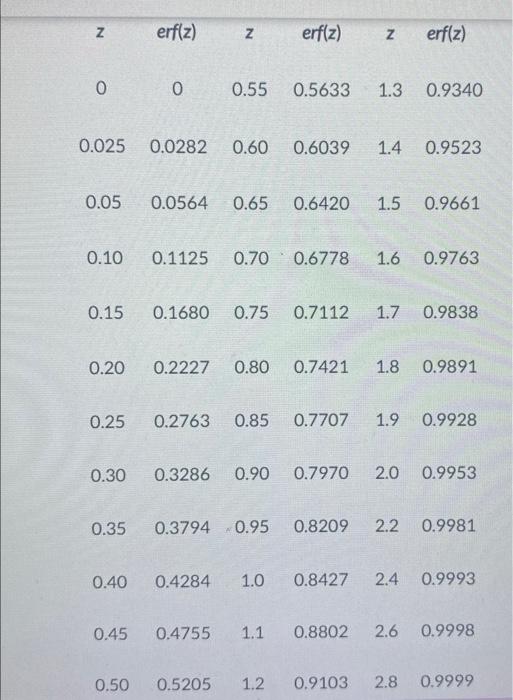
Determine the carburizing time (in s) necessary to achieve a carbon concentration of \( 0.44 \) wt \( \% \) at a position \( 2.0 \mathrm{~mm} \) into an ironcarbon alloy that initially contains \( 0.031 \) wt\% \( \mathrm{C} \). The surface concentration is to be maintained at \( 1.2 \mathrm{wt} \% \mathrm{C} \), and the treatment is to be conducted at \( 1040^{\circ} \mathrm{C} \). Assume that \( D_{0}=5.1 \times 10^{-5} \mathrm{~m}^{2} / \mathrm{s} \) and \( Q_{d}=154 \mathrm{~kJ} / \mathrm{mol} \). You will find the table below useful. \( \begin{array}{llllll}z & \operatorname{erf}(z) \quad z & \operatorname{erf}(z) & z & \operatorname{erf}(z)\end{array} \) \( \begin{array}{llllll}0 & 0 & 0.55 & 0.5633 & 1.3 & 0.9340\end{array} \) \( \begin{array}{llllll}0.025 & 0.0282 & 0.60 & 0.6039 & 1.4 & 0.9523\end{array} \) \( \begin{array}{llllll}0.05 & 0.0564 & 0.65 & 0.6420 & 1.5 & 0.9661\end{array} \) \( \begin{array}{llllll}0.10 & 0.1125 & 0.70 & 0.6778 & 1.6 & 0.9763 \\ 0.15 & 0.1680 & 0.75 & 0.7112 & 1.7 & 0.9838\end{array} \) \( \begin{array}{llllll}0.20 & 0.2227 & 0.80 & 0.7421 & 1.8 & 0.9891 \\ 0.25 & 0.2763 & 0.85 & 0.7707 & 1.9 & 0.9928\end{array} \) \( \begin{array}{llllll}0.30 & 0.3286 & 0.90 & 0.7970 & 2.0 & 0.9953 \\ 0.35 & 0.3794 & 0.95 & 0.8209 & 2.2 & 0.9981\end{array} \) \( \begin{array}{llllll}0.40 & 0.4284 & 1.0 & 0.8427 & 2.4 & 0.9993 \\ 0.45 & 0.4755 & 1.1 & 0.8802 & 2.6 & 0.9998 \\ 0.50 & 0.5205 & 1.2 & 0.9103 & 2.8 & 0.9999\end{array} \)