(Solved): Determine if \( b \) is a linear combination of the vectors formed from the columns of the matrix \ ...

Determine if \( b \) is a linear combination of the vectors formed from the columns of the matrix \( A \). \[ A=\left[\begin{array}{rrr} 1 & -3 & 4 \\ 0 & 5 & 3 \\ -3 & 9 & -12 \end{array}\right], b=\left[\begin{array}{r} 4 \\ -5 \\ -4 \end{array}\right] \] Choose the correct answer below. A. Vector \( \mathrm{b} \) is a linear combination of the vectors formed from the columns of the matrix \( \mathrm{A} \). The pivots in the corresponding echelon matrix are in the first entry in the first column and the third entry in the second column, and the third entry in the third column. B. Vector \( \mathrm{b} \) is a linear combination of the vectors formed from the columns of the matrix A. The pivots in the corresponding echelon matrix are in the first entry in the first column, the second entry in the second column, and the third entry in the fourth column. C. Vector \( b \) is a linear combination of the vectors formed from the columns of the matrix A. The pivots in the corresponding echelon matrix are in the first entry in the first column, the second entry in the second column, and the third entry in the third column. D. Vector \( \mathbf{b} \) is not a linear combination of the vectors formed from the columns of the matrix \( A \). 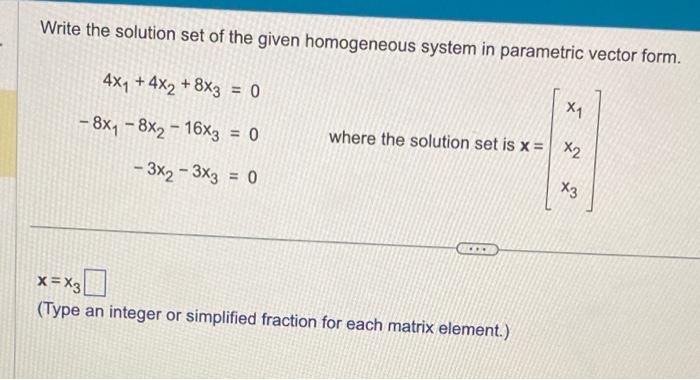Write the solution set of the given homogeneous system in parametric vector form. \[ \begin{array}{r} 4 x_{1}+4 x_{2}+8 x_{3}=0 \\ -8 x_{1}-8 x_{2}-16 x_{3}=0 \\ -3 x_{2}-3 x_{3}=0 \end{array} \] where the solution set is \( \mathrm{x}=\quad \mathrm{x}_{2} \) \[ x=x_{3} \] (Type an integer or simplified fraction for each matrix element.) Describe all solutions of \( \mathrm{Ax}=0 \) in parametric vector form, where \( \mathrm{A} \) is row equivalent to the given matrix. \[ \left[\begin{array}{rrrrrr} 1 & 0 & -1 & 4 & -2 & -5 \\ 0 & 0 & 1 & 0 & 0 & -3 \\ 0 & 0 & 0 & 0 & 1 & -6 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] \] \[ x=x_{2} \quad+x_{4} \quad+x_{6} \] (Type an integer or fraction for each matrix element.)