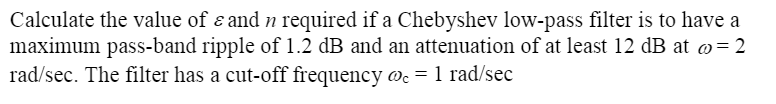(Solved): Could I please have the worked solution to the following question:  A Chebyshev filter ...

Could I please have the worked solution to the following question: 

A Chebyshev filter is described by a squared-magnitude function: \[ |G(j \omega)|^{2}=\frac{1}{1+\varepsilon^{2}\left[C_{\mathrm{n}}\left(\frac{\omega}{\omega_{\mathrm{c}}}\right)\right]^{2}} \] where \( \varepsilon \) is the ripple factor and \( \omega_{c} \) is the cut-off frequency of the filter. The \( n^{\text {th }} \) order Chebyshev polynomial, \( C_{n}\left(\frac{\omega}{\omega_{c}}\right) \), for \( \frac{\omega}{\omega_{c}} \leq 1 \) is defined as: \[ C_{n}\left(\frac{\omega}{\omega_{c}}\right)=\cos \left(n \cos ^{-1}\left(\frac{\omega}{\omega_{c}}\right)\right) \] Prove that in the stop-band of the filter the attenuation, at a given frequency \( \omega \), is approximately given by: \[ X(\text { in } \mathrm{dB}) \cong 20 \log _{10} \varepsilon+6(n-1)+20 n \log _{10}\left(\frac{\omega}{\omega_{c}}\right) \] Make the assumption that for large values of \( \omega \) (in the stop-band of the filter) the following approximation of an \( n^{\text {th }} \) order Chebyshev polynomial is valid: \[ C_{n}\left(\frac{\omega}{\omega_{c}}\right) \cong 2^{n-1}\left(\frac{\omega}{\omega_{c}}\right)^{n} \] Calculate the value of \( \varepsilon \) and \( n \) required if a Chebyshev low-pass filter is to have a maximum pass-band ripple of \( 1.2 \mathrm{~dB} \) and an attenuation of at least \( 12 \mathrm{~dB} \) at \( \omega=2 \) \( \mathrm{rad} / \mathrm{sec} \). The filter has a cut-off frequency \( \omega_{\mathrm{c}}=1 \mathrm{rad} / \mathrm{sec} \) Determine the analogue transfer function, \( G(s) \), of a second order, i.e. \( n=2 \), Chebyshev low-pass filter. Note: Use should be made of the following relations between the Butterworth and Chebyshev pole locations for an \( n^{\text {th }} \) order filter: \( \operatorname{Re}\left[\right. \) Chebyshev \( \left._{1}\right]=\operatorname{Re}\left[\right. \) Butterworth \( \left._{n}\right] x \tanh A \) \( \operatorname{Im}\left[\right. \) Chebyshev \( \left._{1}\right]=\operatorname{Re}\left[\right. \) Butterworth \( \left._{n}\right] \) Chebyshev2 \( = \) Chebyshev1 \( x \cosh A \) (where: \( A=\frac{1}{n} \sinh ^{-1}\left(\frac{1}{\varepsilon}\right) \) ) and also the fact that for a Butterworth filter of order \( n \), the angle of the \( k^{\text {th }} \) pole, \( \phi \mathrm{k} \), to the real axis of the \( s \)-domain is given by: \( \phi_{k}=\left.\frac{k \pi}{n}\right|_{\text {nodd }} \) or \( \phi_{k}=\left.\frac{\left(k+\frac{1}{2}\right) \pi}{n}\right|_{\text {neven }} \)