(Solved): Consider the same RLC circuit in Homework 1, as shown in Figure 1. You have derived the linear diff ...

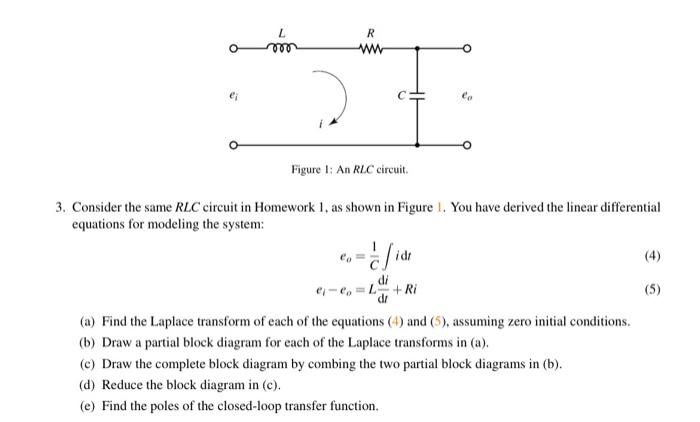
Consider the same RLC circuit in Homework 1, as shown in Figure 1. You have derived the linear differential equations for modeling the system: \[ \begin{aligned} e_{0} &=\frac{1}{C} \int i \mathrm{~d} t \\ e_{i}-e_{o} &=L \frac{\mathrm{d} i}{\mathrm{~d} t}+R i \end{aligned} \] (a) Find the Laplace transform of each of the equations (4) and (5), assuming zero initial conditions. (b) Draw a partial block diagram for each of the Laplace transforms in (a). (c) Draw the complete block diagram by combing the two partial block diagrams in (b). (d) Reduce the block diagram in (c). (e) Find the poles of the closed-loop transfer function.