(Solved): Consider an object moving along a line with the following velocity and initial position. v(t) = -13+ ...

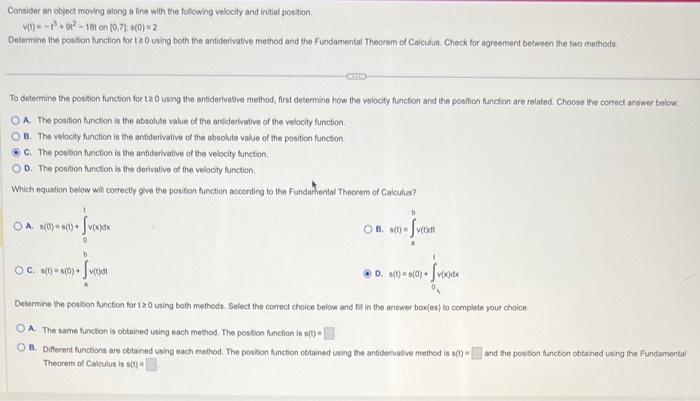
Considec an object moving along s line with the folowing velocity and intial positon. \[ v(t)=-t^{3}+9^{2}-16 t \text { on }(0,7) ; s(0)=2 \] Determine the posston function for 120 using both the antiderivative mothod and the Fundamental Theorem of Caiculua. Check for agreement between the fwo mechods To dotermine the position function for t 20 using the antiderivative method, first determine how the velocity function and the position function are related. Choose the correct answer below. A. The position function is the absolute value of the antiderivative of the velocity function. B. The velocity function is the antiderivative of the absolute value of the position function. C. The position function is the antiderivative of the velocity function. D. The position function is the dertvative of the velocity function. Which equation bolow will correctly give the poston function according to the Fundamental Theorem of Calculus? A. \( s(0)=s(0)+\int_{0}^{1} v(x) d x \) D. \( a(t)=\int_{a}^{D} v(t) d t \) C. \( s(t)=s(0)+\int_{s}^{b} v(f) d t \) D. \( s(t)=s(0) \cdot \int_{0}^{1} v(x) d x \) Delermine the potition function for \( 1 \geq 0 \) uting both mothods. Select the coerect chaice bolow and fil in the answer box[(as) to coenplete your choice. A. The same furction is obtained using each method. The postion function is stb= B. Different functions are cbtained using each method. The poskon function obtained using the antidenivative method is s(t) = and the posibon function obtained using the Fundamental Theorem of Calculus is s(t) \( = \)