(Solved): A table of the ClebschGordan coefficients is seen from the following way: the numbers outsid ...
A table of the Clebsch–Gordan coefficients is seen from the following way:
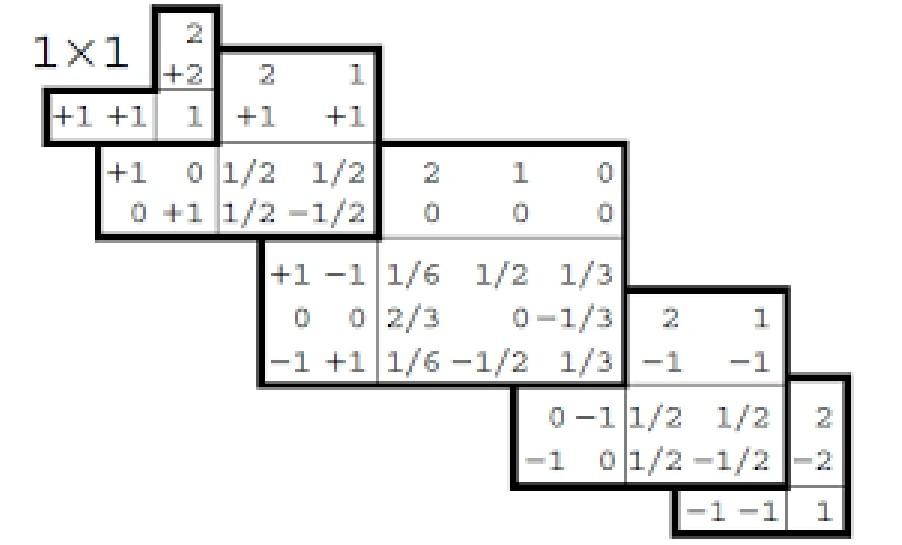
the numbers outside the table represent the angular moments that are being added, so in this case, the table represents the sum of two angular moments such that j1=1 and j2=1.
a) What are the possible values that the total angular momentum j and its projection on the z, mj coordinate, mj, can take?
b) How is the state |2, 2⟩ represented in terms of the states |1, m1⟩|1, m2⟩?
c) Apply the operator J_ to the state |2, 2⟩ and obtain the form of the state |2, 1⟩.
d) Find the form of the state |1, 1⟩.
e) Now compare your results with the table. Note that the columns represent the total angular momentum states, while the rows represent m1 and m2. Using this table, write the form of the states |2, 0⟩, |1, 0⟩, |0, 0⟩.
f) The table can also be read in reverse, so that you can write the states |1, m1⟩|1, m2⟩ in terms of the states of total angular momentum. Using this, suppose you measure m1 and m2 and get 1 and -1 respectively, what is the probability that the total angular momentum of the system is j = 1?
please answer step by step in detail to understand better
thnk u!!
Expert Answer
a) The possible values that the total angular momentum j can take are given by the values that appear in the first column of the table, namely j=0 and j=2. The projection of the total angular momentum on the z-axis, mj, can take values between -j and j in integer steps, so in this case, mj can take the values -2, -1, 0, 1, and 2.b) The state |2,2? corresponds to the case where both individual angular momenta are aligned with the z-axis, i.e., m1=1 and m2=1. From the table, we see that the only non-zero Clebsch-Gordan coefficient for j1=1, j2=1, j=2, m1=1, and m2=1 is C(1,1;1,1|2,2)=1. Therefore, we can write: The Clebsch-Gordan coefficients relate the states of total angular momentum to the states of individual angular momenta.The table in the problem represents the sum of two angular moments, with j1=1 and j2=1.The possible values that the total angular momentum j and its projection on the z, mj coordinate, mj, can take are given by the columns and rows of the table, respectively.