Home /
Expert Answers /
Advanced Math /
a-spring-with-a-8-kg-mass-and-a-damping-constant-16-can-be-held-stretched-1-meters-beyond-its-natura-pa187
(Solved): A spring with a 8-kg mass and a damping constant 16 can be held stretched 1 meters beyond its natura ...
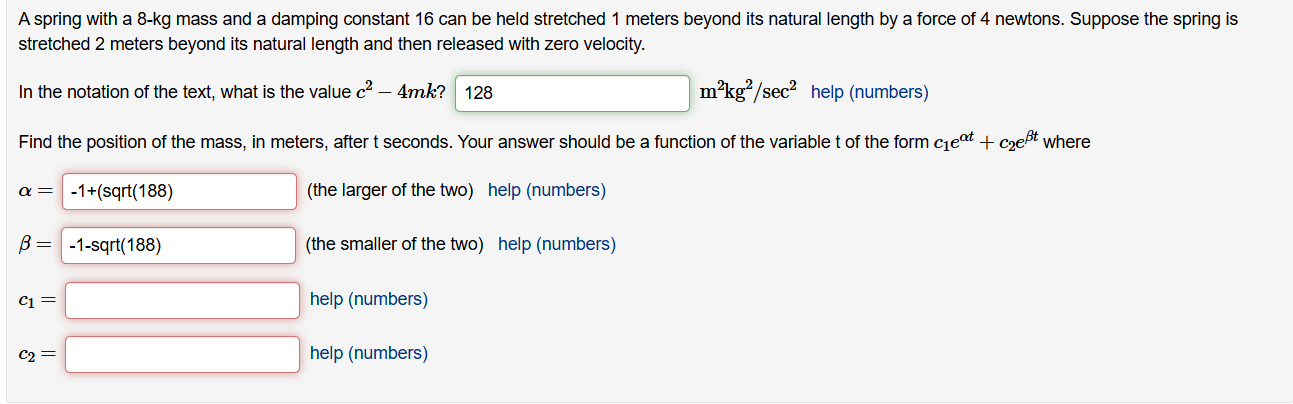
A spring with a 8-kg mass and a damping constant 16 can be held stretched 1 meters beyond its natural length by a force of 4 newtons. Suppose the spring is
stretched 2 meters beyond its natural length and then released with zero velocity.
In the notation of the text, what is the value c^(2)-4mk ?
m^(2)k(g^(2))/(sec^(2)) help (numbers)
Find the position of the mass, in meters, after t seconds. Your answer should be a function of the variable t of the form c_(1)e^(\alpha t)+c_(2)e^(\beta t) where
\alpha =
(the larger of the two) help (numbers)
\beta =
(the smaller of the two) help (numbers)
c_(1)=
help (numbers)
c_(2)=
help (numbers)