(Solved): A simply supported beam \( \mathrm{ABCD} \) is subjected to a linearly distributed load, with \( \ ...

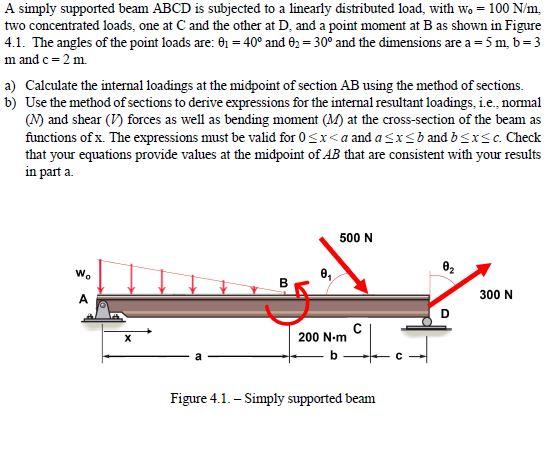
A simply supported beam \( \mathrm{ABCD} \) is subjected to a linearly distributed load, with \( \mathrm{w}_{0}=100 \mathrm{~N} / \mathrm{m} \), two concentrated loads, one at \( \mathrm{C} \) and the other at \( \mathrm{D} \), and a point moment at \( \mathrm{B} \) as shown in Figure 4.1. The angles of the point loads are: \( \theta_{1}=40^{\circ} \) and \( \theta_{2}=30^{\circ} \) and the dimensions are \( a=5 \mathrm{~m}, \mathrm{~b}=3 \) \( \mathrm{m} \) and \( \mathrm{c}=2 \mathrm{~m} \). a) Calculate the internal loadings at the midpoint of section \( A B \) using the method of sections. b) Use the method of sections to derive expressions for the internal resultant loadings, i.e., normal \( (N) \) and shear \( (V) \) forces as well as bending moment \( (M) \) at the cross-section of the beam as functions of \( \mathrm{x} \). The expressions must be valid for \( 0 \leq x