(Solved): A sailboat is moving at a constant velocity due north, as depicted in the figure. The water exerts ...

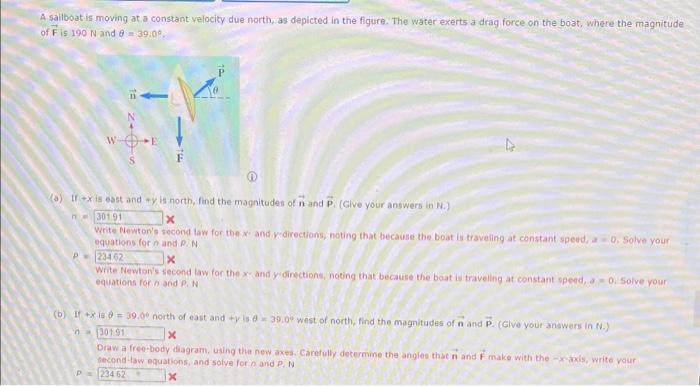
A sailboat is moving at a constant velocity due north, as depicted in the figure. The water exerts a drag force on the boat, where the magnitude of \( \vec{F} / 5190 \mathrm{~N} \) and \( \theta=39.0^{\circ} \). (a) If \( +x \) is east and \( +y \) is north, find the magnitudes of \( \vec{n} \) and \( \vec{p} \), (Glve your answers in \( N \).) \( n= \) Write Newton's second law for the \( x \) 'and yedirections, noting that because the boat is traveling at constant speud, a a 0 , Solve your equations for \( n \) and D. \( N \). \( p= \) \( \times \) Write Newton's thecond law for the \( x \) - and \( y \) directions, noting that because the boat is traveling at constant opend, a \( =0 \). solve your equations for \( n \) and \( P_{1}, \mathrm{~N} \) (b) If \( +x \) is \( \vec{\theta}=39,00^{\circ} \) north of east and \( +y \sin \theta=39,0^{4} \) west of north, find the magnitudes of \( \vec{n} \) and \( \overrightarrow{\mathrm{p}} \). (Clive yout answers in \( \mathrm{N} \).) Draw a free-body diagram, ualing thit new axes. Carefully determine the angies that \( \vec{n} \) and \( \vec{F} \) make with the \( -x \times 2 \times i s \), write vour fercond-1aw eguations, and solve for in and P. N