(Solved): A pediatrician wants to determine the relation that may exist between a child's height and head cir ...

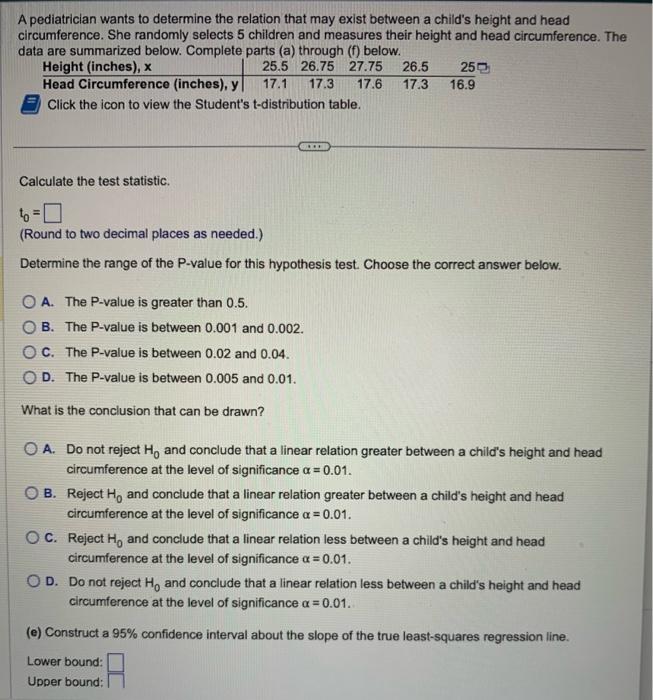
A pediatrician wants to determine the relation that may exist between a child's height and head circumference. She randomly selects 5 children and measures their height and head circumference. The data are summarized below. Complete parts (a) through (f) below. Click the icon to view the Student's t-distribution table. Calculate the test statistic. \[ t_{0}= \] (Round to two decimal places as needed.) Determine the range of the P-value for this hypothesis test. Choose the correct answer below. A. The P-value is greater than \( 0.5 \). B. The P-value is between \( 0.001 \) and \( 0.002 \). C. The P-value is between \( 0.02 \) and \( 0.04 \). D. The P-value is between \( 0.005 \) and \( 0.01 \). What is the conclusion that can be drawn? A. Do not reject \( \mathrm{H}_{0} \) and conclude that a linear relation greater between a child's height and head circumference at the level of significance \( \alpha=0.01 \). B. Reject \( \mathrm{H}_{0} \) and conclude that a linear relation greater between a child's height and head circumference at the level of significance \( \alpha=0.01 \). C. Reject \( \mathrm{H}_{0} \) and conclude that a linear relation less between a child's height and head circumference at the level of significance \( \alpha=0.01 \). D. Do not reject \( \mathrm{H}_{0} \) and conclude that a linear relation less between a child's height and head circumference at the level of significance \( \alpha=0.01 \). (e) Construct a \( 95 \% \) confidence interval about the slope of the true least-squares regression line. 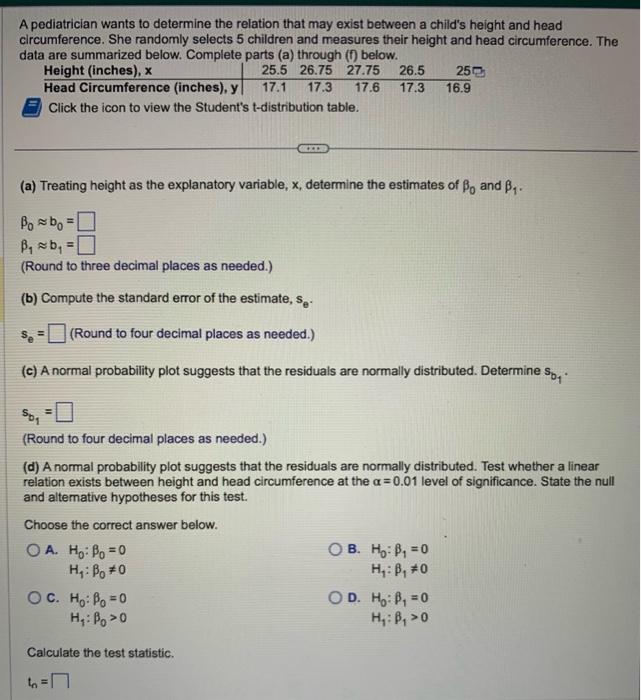Lower bound: Upper bound: A pediatrician wants to determine the relation that may exist between a child's height and head circumference. She randomly selects 5 children and measures their height and head circumference. The data are summarized below. Complete parts (a) through (f) below. Click the icon to view the Student's t-distribution table. (a) Treating height as the explanatory variable, \( x \), determine the estimates of \( \beta_{0} \) and \( \beta_{1} \). \[ \begin{array}{l} \beta_{0} \approx b_{0}= \\ \beta_{1} \approx b_{1}= \end{array} \] (Round to three decimal places as needed.) (b) Compute the standard error of the estimate, \( \mathrm{s}_{\mathrm{e}^{*}} \). \( S_{e}=\quad \) (Round to four decimal places as needed.) (c) A normal probability plot suggests that the residuals are normally distributed. Determine \( s_{b_{1}} \). \[ \mathrm{s}_{\mathrm{b}_{1}}= \] (Round to four decimal places as needed.) (d) A normal probability plot suggests that the residuals are normally distributed. Test whether a linear relation exists between height and head circumference at the \( \alpha=0.01 \) level of significance. State the null and altemative hypotheses for this test. Choose the correct answer below. A. \( \mathrm{H}_{0}: \beta_{0}=0 \) B. \( H_{0}: \beta_{1}=0 \) \( H_{1}: \beta_{0} \neq 0 \) \( H_{1}: \beta_{1} \neq 0 \) c. \( \mathrm{H}_{0}: \beta_{0}=0 \) D. \( H_{0}: \beta_{1}=0 \) \( H_{f}: \beta_{0}>0 \) \( H_{1}: \beta_{1}>0 \) Calculate the test statistic. 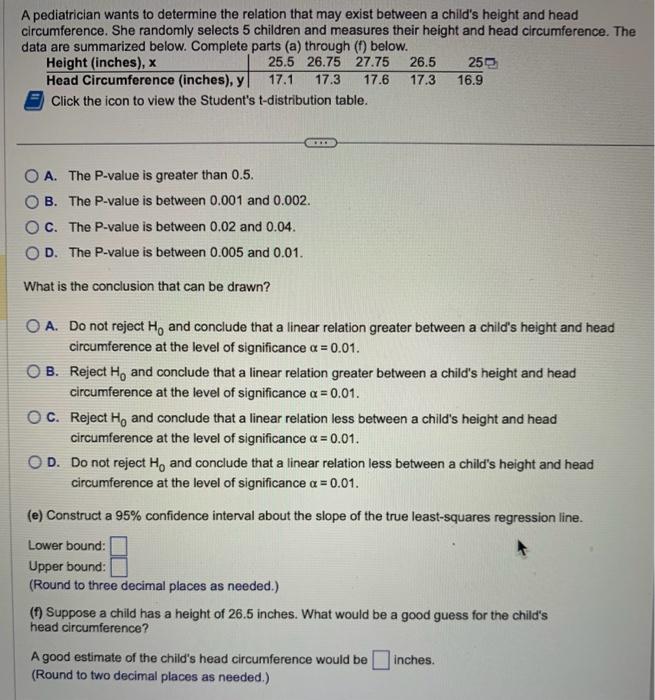\[ t_{n}= \] A pediatrician wants to determine the relation that may exist between a child's height and head circumference. She randomly selects 5 children and measures their height and head circumference. The data are summarized below. Complete parts (a) through (f) below. Click the icon to view the Student's t-distribution table. A. The P-value is greater than 0.5. B. The P-value is between \( 0.001 \) and \( 0.002 \). C. The P-value is between \( 0.02 \) and \( 0.04 \). D. The P-value is between \( 0.005 \) and \( 0.01 \). What is the conclusion that can be drawn? A. Do not reject \( \mathrm{H}_{0} \) and conclude that a linear relation greater between a child's height and head circumference at the level of significance \( \alpha=0.01 \). B. Reject \( \mathrm{H}_{0} \) and conclude that a linear relation greater between a child's height and head circumference at the level of significance \( \alpha=0.01 \). C. Reject \( \mathrm{H}_{0} \) and conclude that a linear relation less between a child's height and head circumference at the level of significance \( \alpha=0.01 \). D. Do not reject \( \mathrm{H}_{0} \) and conclude that a linear relation less between a child's height and head circumference at the level of significance \( \alpha=0.01 \). (e) Construct a \( 95 \% \) confidence interval about the slope of the true least-squares regression line. Lower bound: Upper bound: (Round to three decimal places as needed.) (f) Suppose a child has a height of \( 26.5 \) inches. What would be a good guess for the child's head circumference? A good estimate of the child's head circumference would be (Round to two decimal places as needed.)