(Solved): A gearbox shaft is shown in Figure 6. The forces shown are the tangential forces where the gears mes ...

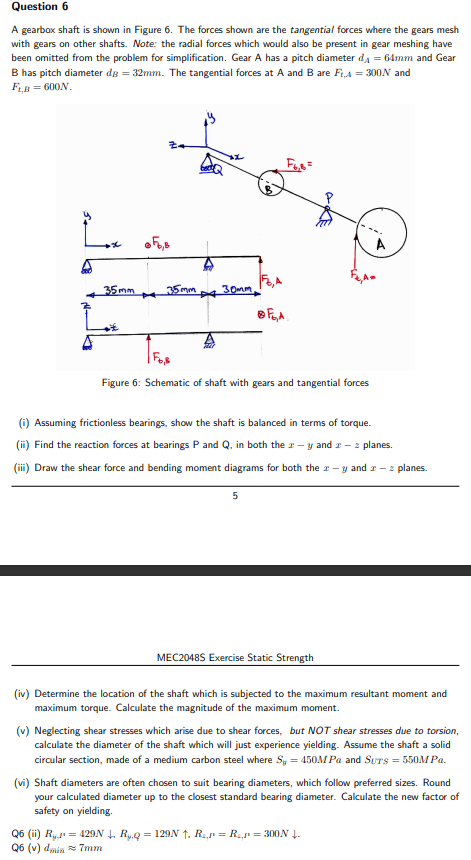
A gearbox shaft is shown in Figure 6. The forces shown are the tangential forces where the gears mesh with gears on other shafts. Note: the radial forces which would also be present in gear meshing have been omitted from the problem for simplification. Gear A has a pitch diameter dA = 64mm and Gear B has pitch diameter dB = 32mm. The tangential forces at A and B are Ft,A = 300N and Ft,B = 600N.

A gearbox shaft is shown in Figure 6. The forces shown are the tangential forces where the gears mesh with gears on other shafts. Note: the radial forces which would also be present in gear meshing have been omitted from the problem for simplification. Gear A has a pitch diameter \( d_{A}=64 \mathrm{~mm} \) and Gear \( \mathrm{B} \) has pitch diameter \( d_{B}=32 \mathrm{~mm} \). The tangential forces at \( \mathrm{A} \) and \( \mathrm{B} \) are \( F_{t, A}=300 \mathrm{~N} \) and \( F_{t, B}=600 N \). Figure 6: Schematic of shaft with gears and tangential forces (i) Assuming frictionless bearings, show the shaft is balanced in terms of torque. (ii) Find the reaction forces at bearings \( \mathrm{P} \) and \( \mathrm{Q} \), in both the \( x-y \) and \( x-z \) planes. (iii) Draw the shear force and bending moment diagrams for both the \( x-y \) and \( x-z \) planes. 5 MEC2048S Exercise Static Strength (iv) Determine the location of the shaft which is subjected to the maximum resultant moment and maximum torque. Calculate the magnitude of the maximum moment. (v) Neglecting shear stresses which arise due to shear forces, but NOT shear stresses due to torsion, calculate the diameter of the shaft which will just experience yielding. Assume the shaft a solid circular section, made of a medium carbon steel where \( S_{\mathrm{g}}=450 \mathrm{MPa} \) and \( S U T \mathrm{~S}=550 \mathrm{MPa} \). (vi) Shaft diameters are often chosen to suit bearing diameters, which follow preferred sizes. Round your calculated diameter up to the closest standard bearing diameter. Calculate the new factor of safety on yielding. Q6 (ii) \( R_{i,}, r^{\prime}=429 N \downarrow R_{i, Q}=129 N \uparrow, R_{\varepsilon, I^{*}}=R_{\varepsilon, N^{*}}=300 \mathrm{~N} \downarrow \). \( \mathrm{Q} 6 \) (v) \( d_{\min } \approx 7 \mathrm{~mm} \)