(Solved): A free body diagram for the gate and water along with the forces is shown below: (a) In terms ...

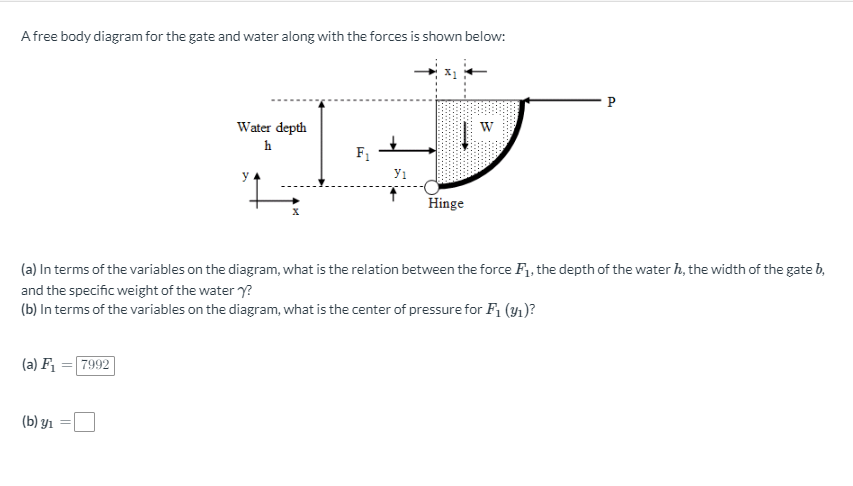
A free body diagram for the gate and water along with the forces is shown below: (a) In terms of the variables on the diagram, what is the relation between the force \( F_{1} \), the depth of the water \( h \), the width of the gate \( b \), and the specific weight of the water \( \gamma \) ? (b) In terms of the variables on the diagram, what is the center of pressure for \( F_{1}\left(y_{1}\right) \) ? (a) What is the specific weight of water? (b) What is the magnitude of the force \( F_{1} \) ? (c) What is the distance \( y_{1} \) ? (a) \( y= \) \( \mathrm{lbf} / \mathrm{ft}^{3} \) (b) \( F_{1}= \) Ibf (c) \( y_{1}= \) \( \mathrm{ft} \) (a) In terms of the variables on the diagram and fluid properties, what is the weight of the water inside the free body diagram? (b) In terms of the variables on the diagram, what is the distance \( x_{1} \) ? (a) \( W= \) (b) \( x_{1}= \) (a) What is the weight of the water inside the free body diagram? (b) What is the distance \( x_{1} \) ? 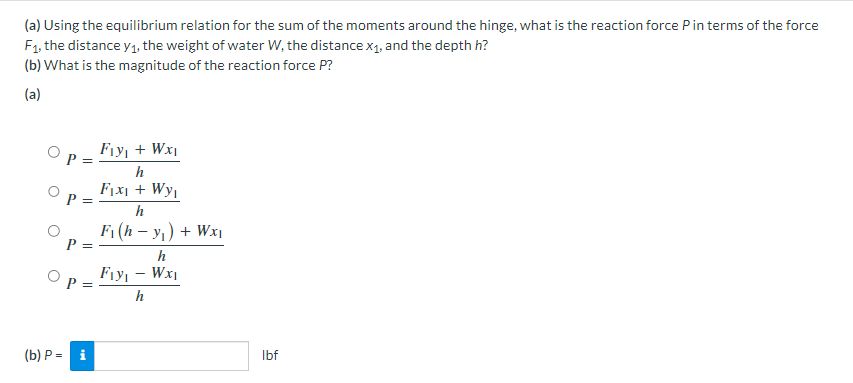(a) \( \mathrm{W}= \) Ibf (b) \( x_{1}= \) \( \mathrm{ft} \) (a) Using the equilibrium relation for the sum of the moments around the hinge, what is the reaction force \( P \) in terms of the force \( F_{1} \), the distance \( y_{1} \), the weight of water \( W \), the distance \( x_{1} \), and the depth \( h \) ? (b) What is the magnitude of the reaction force \( P \) ? (a) \[ \begin{aligned} P &=\frac{F_{1} y_{1}+W x_{1}}{h} \\ P &=\frac{F_{1} x_{1}+W y_{1}}{h} \\ P &=\frac{F_{1}\left(h-y_{1}\right)+W x_{1}}{h} \\ P &=\frac{F_{1} y_{1}-W x_{1}}{h} \end{aligned} \] (b) \( P= \) Ibf