(Solved): (a) Find the value of \( c \) that satisfies the conclusion of the Mean Value Theorem for the funct ...

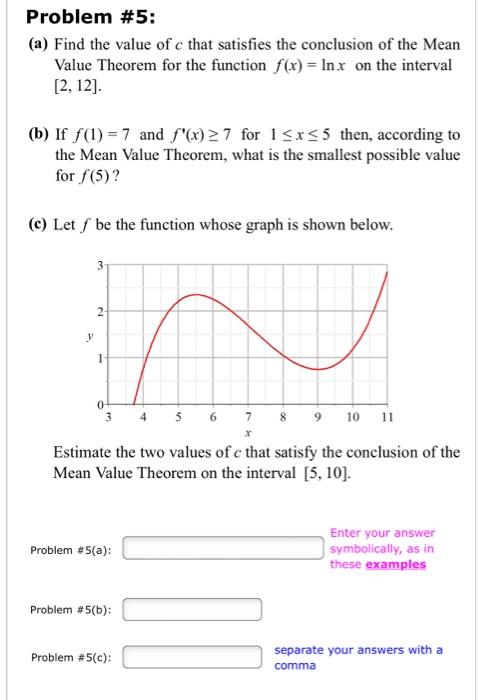
(a) Find the value of \( c \) that satisfies the conclusion of the Mean Value Theorem for the function \( f(x)=\ln x \) on the interval \( [2,12] \) (b) If \( f(1)=7 \) and \( f^{\prime}(x) \geq 7 \) for \( 1 \leq x \leq 5 \) then, according to the Mean Value Theorem, what is the smallest possible value for \( f(5) \) ? (c) Let \( f \) be the function whose graph is shown below. Estimate the two values of \( c \) that satisfy the conclusion of the Mean Value Theorem on the interval \( [5,10] \). \( \begin{array}{ll}\text { Problem #S(a): } & \text { Enter your answer } \\ & \text { symbolically, as in } \\ \text { these examples }\end{array} \) Problem #5(b): Problem \( \# 5(c) \) : separate your answers with a comma