(Solved): (a) Figure 1 shows a simple state machine, with a single input, A, a single o ...

???????

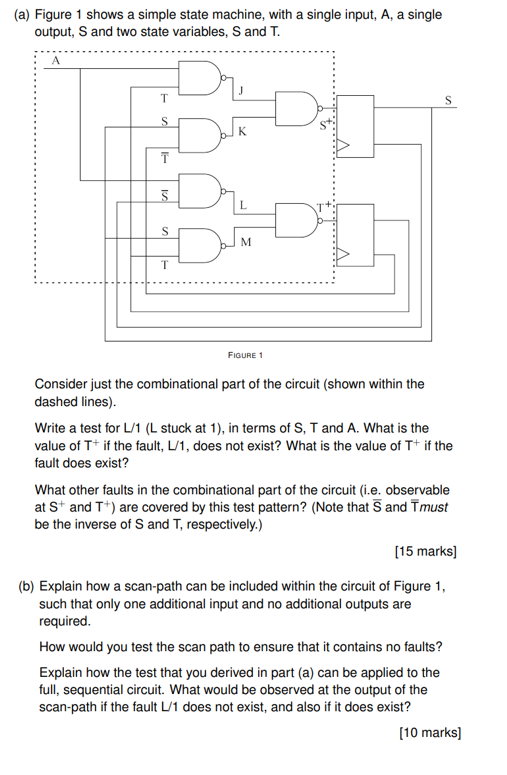
(a) Figure 1 shows a simple state machine, with a single input, A, a single output, \( \mathrm{S} \) and two state variables, \( \mathrm{S} \) and \( \mathrm{T} \). Consider just the combinational part of the circuit (shown within the dashed lines). Write a test for \( L / 1 \) ( \( L \) stuck at 1 ), in terms of \( \mathrm{S}, T \) and \( A \). What is the value of \( \mathrm{T}^{+} \)if the fault, \( L / 1 \), does not exist? What is the value of \( \mathrm{T}^{+} \)if the fault does exist? What other faults in the combinational part of the circuit (i.e. observable at \( \mathrm{S}^{+} \)and \( \mathrm{T}^{+} \)) are covered by this test pattern? (Note that \( \overline{\mathrm{S}} \) and \( \overline{\mathrm{T}} \) must be the inverse of \( S \) and \( T \), respectively.) [15 marks] (b) Explain how a scan-path can be included within the circuit of Figure 1, such that only one additional input and no additional outputs are required. How would you test the scan path to ensure that it contains no faults? Explain how the test that you derived in part (a) can be applied to the full, sequential circuit. What would be observed at the output of the scan-path if the fault \( L / 1 \) does not exist, and also if it does exist? [10 marks]