(Solved): A beam is fabricated by bolting together three wood members as shown in the figure and is subjected ...

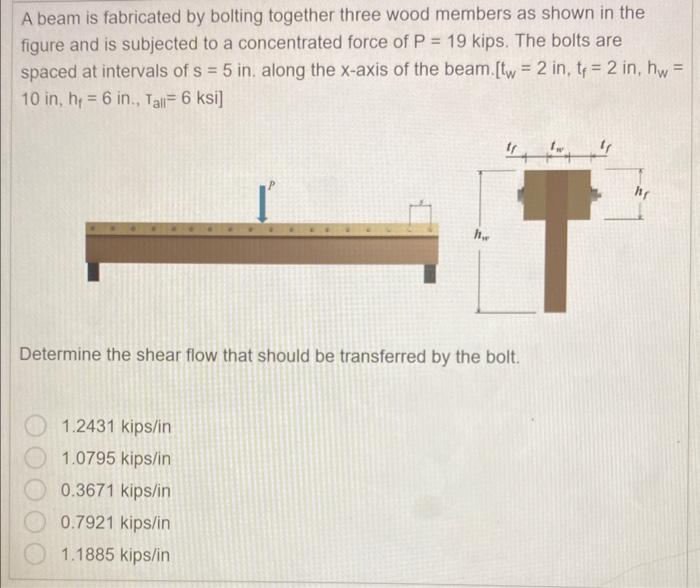
A beam is fabricated by bolting together three wood members as shown in the figure and is subjected to a concentrated force of \( P=19 \) kips. The bolts are spaced at intervals of \( s=5 \) in. along the \( x \)-axis of the beam. \( \left[t_{w}=2\right. \) in, \( t_{f}=2 \) in, \( h_{w}= \) \( \left.10 \mathrm{in}, \mathrm{h}_{\mathrm{f}}=6 \mathrm{in} ., \mathrm{T}_{\text {all }}=6 \mathrm{ksi}\right] \) Determine the shear flow that should be transferred by the bolt. 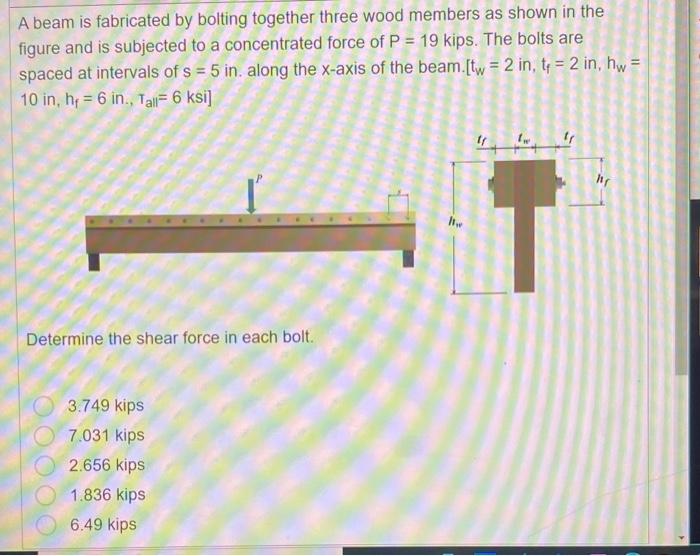\( 1.2431 \mathrm{kips} / \mathrm{in} \) \( 1.0795 \) kips/in \( 0.3671 \mathrm{kips} / \mathrm{in} \) \( 0.7921 \mathrm{kips} / \mathrm{in} \) 1.1885 kips/in A beam is fabricated by bolting together three wood members as shown in the figure and is subjected to a concentrated force of \( P=19 \) kips. The bolts are spaced at intervals of \( s=5 \) in. along the \( x \)-axis of the beam. [t \( w_{w}=2 \) in, \( t_{f}=2 \) in, \( h_{w}= \) 10 in, \( h_{f}=6 \) in., \( \left.T_{\text {all }}=6 \mathrm{ksi}\right] \) Determine the shear force in each bolt. \( 3.749 \) kips 7.031 kips \( 2.656 \) kips \( 1.836 \) kips \( 6.49 \) kips A beam is fabricated by bolting together three wood members as shown in the figure and is subjected to a concentrated force of \( P=19 \) kips. The bolts are spaced at intervals of \( s=5 \) in. along the \( x \)-axis of the beam. [t \( t_{w}=2 \) in, \( t_{f}=2 \) in, \( h_{w}= \) \( 10 \mathrm{in}, \mathrm{h}_{\mathrm{f}}=6 \) in., \( \left.\mathrm{T}_{\text {all }}=6 \mathrm{ksi}\right] \) Calculate the shear stress in the bolts if the bolts have a diameter of \( \mathrm{d}=3 / 4 \) in and are spaced at the interval s. \( 2.07 \mathrm{ksi} \) \( 0.865 \mathrm{ksi} \) \( 3.196 \mathrm{ksi} \) \( 0.199 \mathrm{ksi} \) 4.155 ksi A beam is fabricated by bolting together three wood members as shown in the figure and is subjected to a concentrated force of \( \mathrm{P}=19 \) kips. The bolts are spaced at intervals of \( s=5 \) in. along the \( x \)-axis of the beam. [t \( t_{w}=2 \) in, \( t_{f}=2 \) in, \( h_{w}= \) \( 10 \mathrm{in}, \mathrm{h}_{\mathrm{f}}=6 \) in.., \( \mathrm{Tall}^{\mathrm{al}}=6 \mathrm{ksi} \) ] Determine the required spacing between the bolts if the shear stress in the bolts is limited to Tall:- \[ \begin{array}{l} 6.3 \text { in } \\ 2.2 \text { in } \\ 13.4 \text { in } \\ 3.5 \text { in } \\ 7.2 \text { in } \end{array} \]