(Solved): A 20-meter long beam-tank assembly supports the loading shown in addition to its weight, which is ...

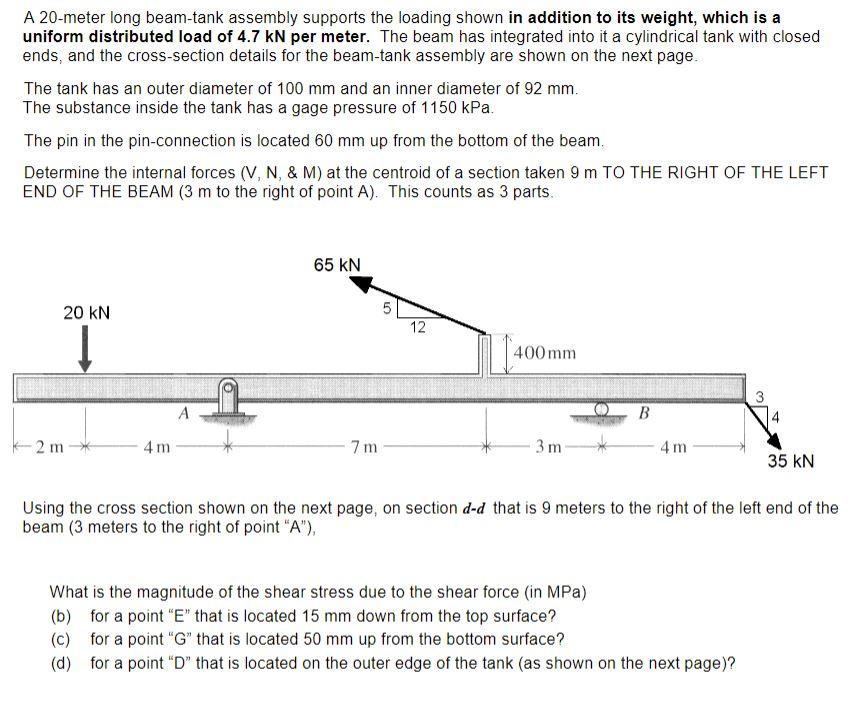
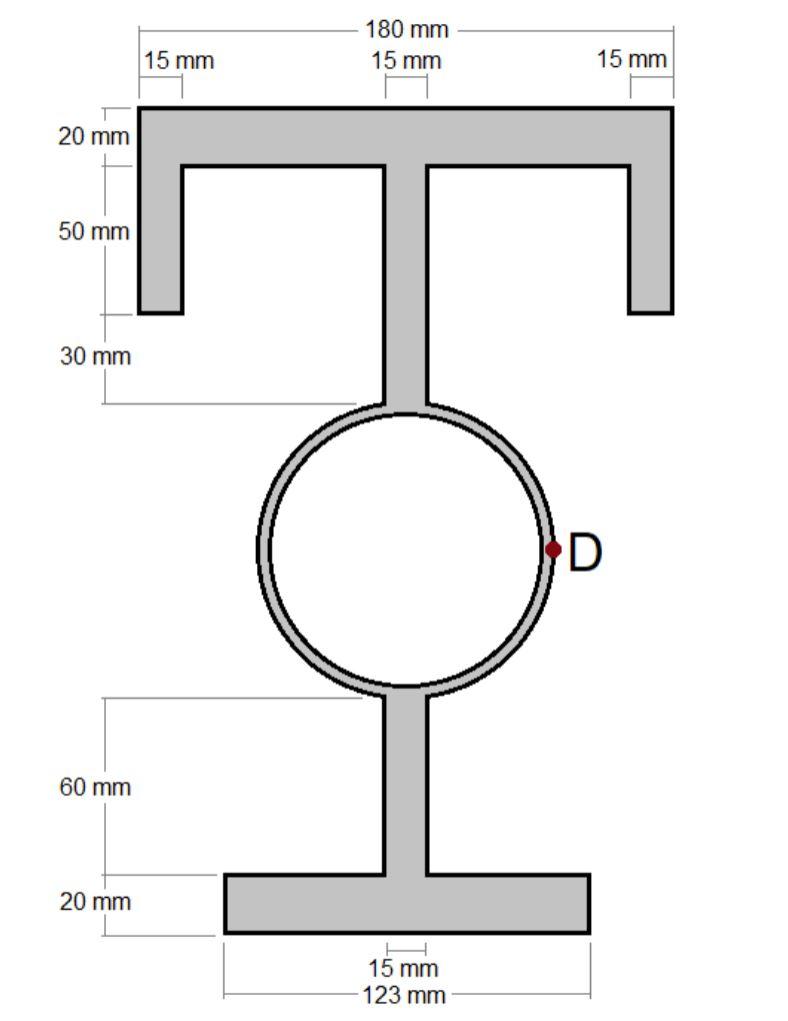
A 20-meter long beam-tank assembly supports the loading shown in addition to its weight, which is a uniform distributed load of \( 4.7 \mathrm{kN} \) per meter. The beam has integrated into it a cylindrical tank with closed ends, and the cross-section details for the beam-tank assembly are shown on the next page. The tank has an outer diameter of \( 100 \mathrm{~mm} \) and an inner diameter of \( 92 \mathrm{~mm} \). The substance inside the tank has a gage pressure of \( 1150 \mathrm{kPa} \). The pin in the pin-connection is located \( 60 \mathrm{~mm} \) up from the bottom of the beam. Determine the internal forces \( (V, N, \& M) \) at the centroid of a section taken \( 9 \mathrm{~m} \) TO THE RIGHT OF THE LEFT END OF THE BEAM \( (3 \mathrm{~m} \) to the right of point \( \mathrm{A}) \). This counts as 3 parts. Using the cross section shown on the next page, on section \( d-d \) that is 9 meters to the right of the left end of the beam ( 3 meters to the right of point " \( A \) "), What is the magnitude of the shear stress due to the shear force (in MPa) (b) for a point " \( E \) " that is located \( 15 \mathrm{~mm} \) down from the top surface? (c) for a point " \( \mathrm{G}^{n} \) that is located \( 50 \mathrm{~mm} \) up from the bottom surface? (d) for a point " \( D \) " that is located on the outer edge of the tank (as shown on the next page)?