Home /
Expert Answers /
Physics /
a-1-65-mathrm-m-thin-brass-rod-is-bent-in-half-to-form-a-right-angled-mathrm-l-as-pa880
(Solved): A \( 1.65 \mathrm{~m} \) thin brass rod is bent in half to form a right-angled \( \mathrm{L} \), as ...
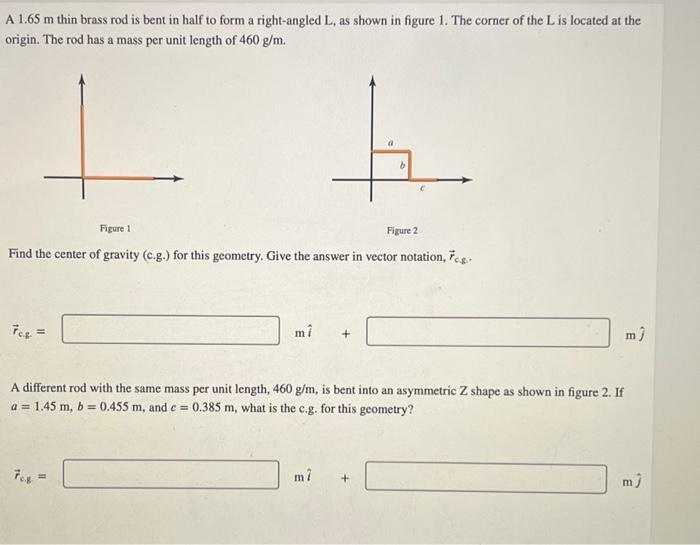
A \( 1.65 \mathrm{~m} \) thin brass rod is bent in half to form a right-angled \( \mathrm{L} \), as shown in figure 1 . The corner of the \( \mathrm{L} \) is located at the origin. The rod has a mass per unit length of \( 460 \mathrm{~g} / \mathrm{m} \). Figure 1 Figure 2 Find the center of gravity (c.g.) for this geometry. Give the answer in vector notation, \( \vec{r}_{\mathrm{cg}} \). \[ \vec{r}_{\mathrm{ce}}=\quad \mathrm{m} \hat{i}+1 \mathrm{~m} \hat{j} \] A different rod with the same mass per unit length, \( 460 \mathrm{~g} / \mathrm{m} \), is bent into an asymmetric \( \mathrm{Z} \) shape as shown in figure 2 . If \( a=1.45 \mathrm{~m}, b=0.455 \mathrm{~m} \), and \( c=0.385 \mathrm{~m} \), what is the c.g. for this geometry? \[ \vec{r}_{\mathrm{c.g}}= \]
Expert Answer
A 1.65 m thin rod is bent into half perpendicularly to form L shape, The center of the L is origin. Since the rod is of uniform density, the center of