Home /
Expert Answers /
Statistics and Probability /
8-calculating-the-probability-of-a-type-ii-error-suppose-an-architectural-firm-specializing-in-the-pa575
(Solved): 8. Calculating the probability of a Type II error Suppose an architectural firm specializing in the ...
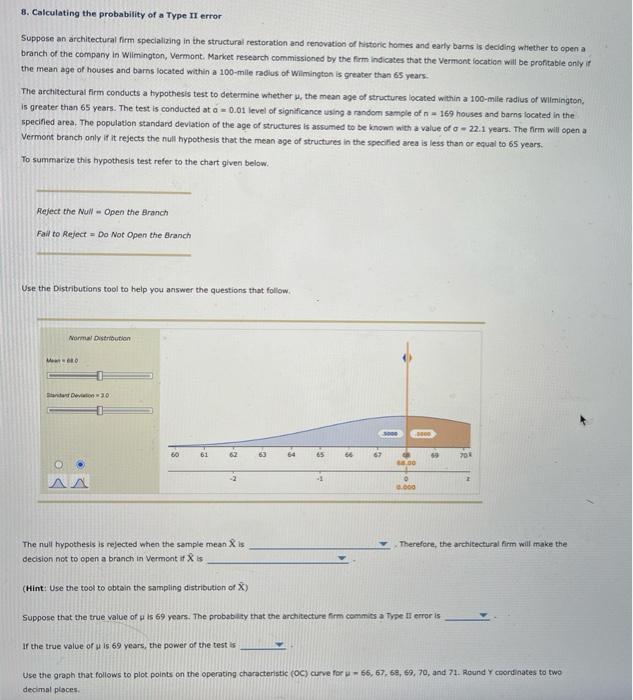
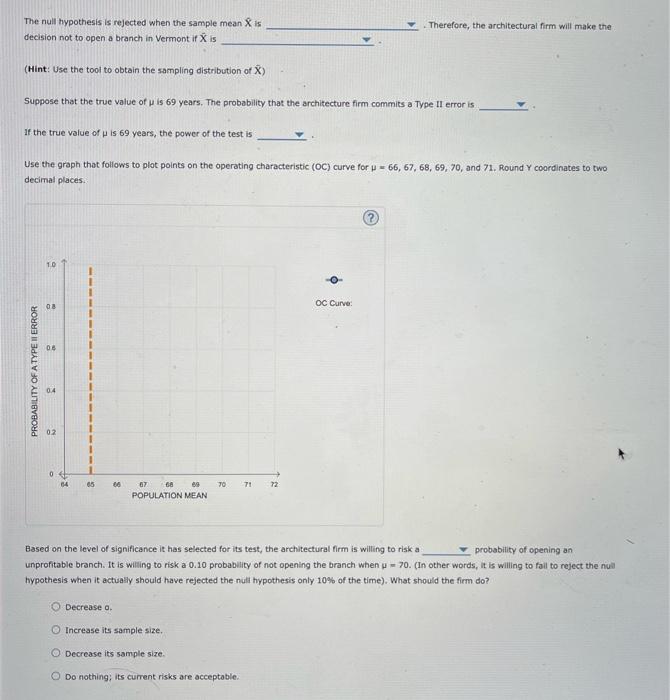
8. Calculating the probability of a Type II error Suppose an architectural firm specializing in the structural restoration and renovation of historic hornes and early bams is deciding witether to apen a branch of the company in Wilmington, Vermont. Market research commissioned by the firm indicates that the Vermont location will be proftable onty if the mean age of houses and barns located within a 100 -mile radius of Wimington is greater than \( 6.5 \) years. The architectural firm conducts a hypothesis test to determine whether \( \mu \), the mean age of structures located within a 100 -milie radius of wilmington, is greater than 65 years. The test is conducted at \( a=0.01 \) level of significance using a random sample of \( n=169 \) houses and barns iocated in the specified area. The population standard deviation of the age of structures is assumed to be known with a value of \( \sigma-22.1 \) years. The firm will open a Vermont branch only if it rejects the null hypothesis that the mean age of structures in the spectied area is less than or equal to 65 years. To summarize this hypothesis test refer to the chart given belaw. Reject the Nuil = Open the Branch Fail to Refect \( = \) Do Not Open the Branch Use the Distributions tool to help you answer the questions that follow. The null hypothesis is rejected when the sample mean \( \hat{X} \) is Therefore, the architectural firm will make the decision not to open a branch in Vermont if \( \hat{X} \) is (Hint: Use the tool to obtain the sampting distribution of \( \overline{\mathrm{X}} \) ) Suppose that the true value of in is 69 years. The probabily that the architecture firm commits a Type II error is If the true value of \( \mu \) is 69 years, the power of the test is Use the graph that follows to plot points on the operating characteristic (oc) curve for \( u=66,67,69,69,70 \), and 71 . Round \( Y \) coordinates to two decimal places.
The null typothesis is rejected when the sample mean \( \bar{X} \) is Therefore, the architectural firm will make the decision not to open a branch in Vermont if \( \bar{X} \) is (Hint: Use the tool to obtain the sampling distribution of \( \bar{X} \) ) Suppose that the true value of \( \mu \) is 69 years. The probability that the architecture firm commits a Type II error is If the true value of \( \mu \) is 69 years, the power of the test is Use the graph that follows to plot points on the operating characteristic (OC) curve for \( \mu=66,67,68,69,70 \), and 71 . Round \( Y \) coardinates to two decimal places. Based on the level of significance it has selected for its test, the architectural firm is willing to risk a probability of opening an unprofitable branch. It is willing to risk a \( 0.10 \) probability of not opening the branch when \( \mu=70 \). (In other words, it is willing to fail to reject the nuil hypothesis when it actually should have rejected the null hypothesis only \( 10 \% \) of the time). What should the firm do? Decrease o. Increase its sample size. Decrease its sample size. Do nothing; its current risks are acceptable.
Expert Answer
Solution : Given data : ?=0.0