(Solved): 5.20 The caustic concentration of the mixing tank shown in Fig. E5.20 is measured using a conductiv ...

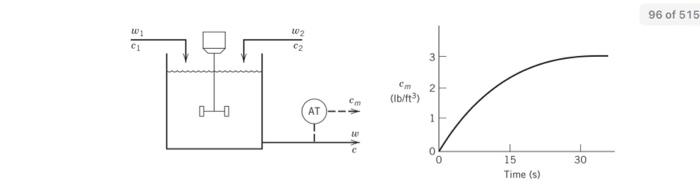
5.20 The caustic concentration of the mixing tank shown in Fig. E5.20 is measured using a conductivity cell. The total volume of solution in the tank is constant at \( 7 \mathrm{ft}^{3} \) and the density \( \left(\rho=70 \mathrm{lb} / \mathrm{ft}^{3}\right) \) can be considered to be independent of concentration. Let \( c_{m} \) denote the caustic concentration measured by the conductivity cell. The dynamic response of the conductivity cell to a step change (at \( t=0) \) of \( 3 \mathrm{lb} / \mathrm{ft}^{3} \) in the actual concentration (passing through the cell) is also shown in Fig. E5.20. 96 of 515 (a) Determine the transfer function \( C_{m}^{\prime}(s) / C_{1}^{\prime}(s) \) assuming that the flow rates are equal and constant: \( \left(w_{1}=w_{2}=5 \mathrm{lb} / \mathrm{min}\right) \). (b) Find the response for a step change in \( c_{1} \) from 14 to \( 17 \mathrm{lb} / \mathrm{ft}^{3} \). (c) If the transfer function \( C_{m}^{\prime}(s) / C^{\prime}(s) \) were approximated by 1 (unity), what would be the step response of the system for the same input change? (d) By comparison of (b) and (c), what can you say about the dynamics of the conductivity cell? Plot both responses, if necessary.