Home /
Expert Answers /
Mechanical Engineering /
3-refer-to-the-linkage-and-its-vector-diagram-below-the-acceleration-equation-for-this-linkage-in-pa469
(Solved): 3. Refer to the linkage and its vector diagram below. The acceleration equation for this linkage in ...
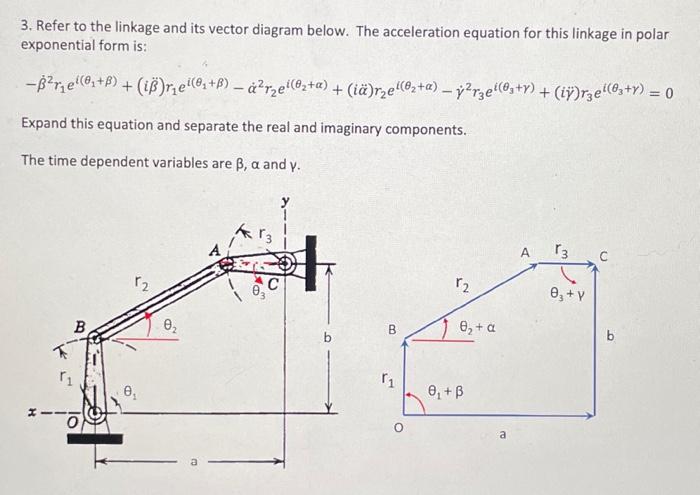
3. Refer to the linkage and its vector diagram below. The acceleration equation for this linkage in polar exponential form is: Expand this equation and separate the real and imaginary components. The time dependent variables are and .