(Solved): 2D Vector Addition sure to include negative sign if value is negative.) Question 29 What is the \( ...

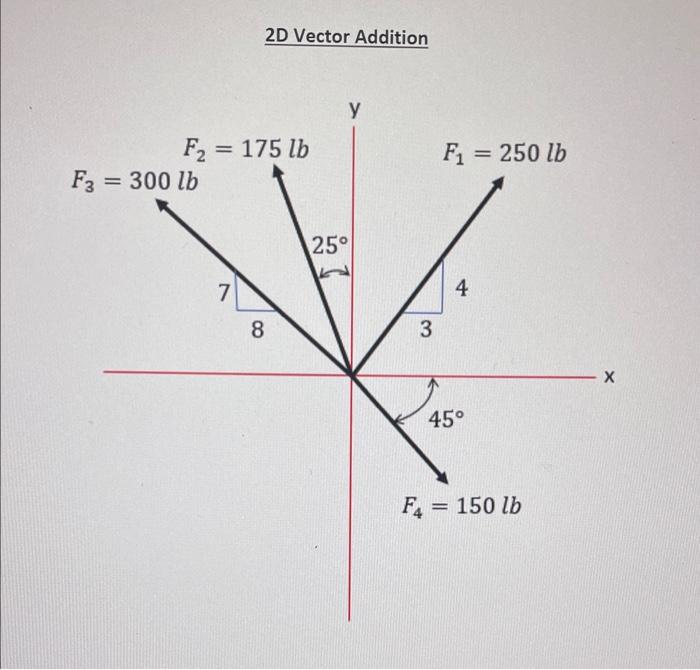
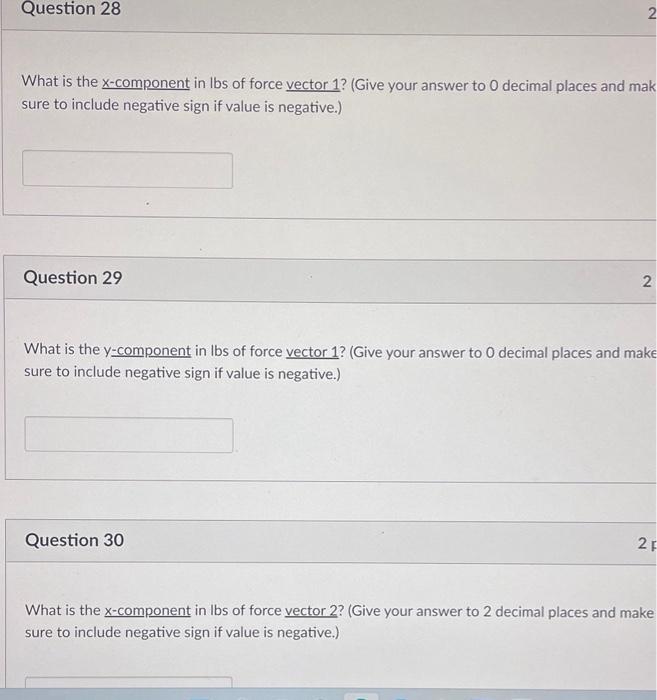
2D Vector Addition sure to include negative sign if value is negative.) Question 29 What is the \( \mathrm{y} \)-component in Ibs of force vector 1 ? (Give your answer to 0 decimal places and maki sure to include negative sign if value is negative.) Question 30 What is the \( \underline{x \text {-component }} \) in Ibs of force vector 2 ? 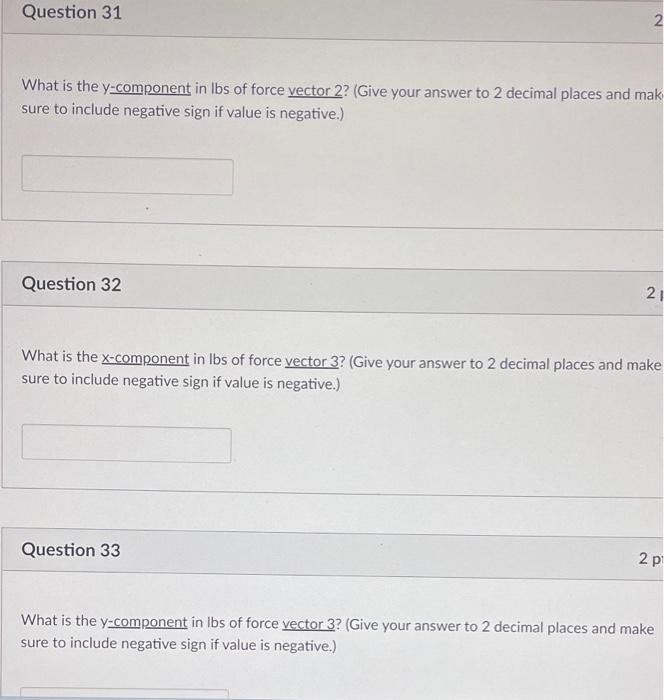(Give your answer to 2 decimal places and make sure to include negative sign if value is negative.) What is the \( \mathrm{y} \)-component in Ibs of force vector 2 ? (Give your answer to 2 decimal places and mak sure to include negative sign if value is negative.) Question 32 What is the \( \underline{x \text {-component }} \) in Ibs of force vector 3 ? (Give your answer to 2 decimal places and make sure to include negative sign if value is negative.) Question 33 What is the \( y \)-component in Ibs of force vector 3 ? 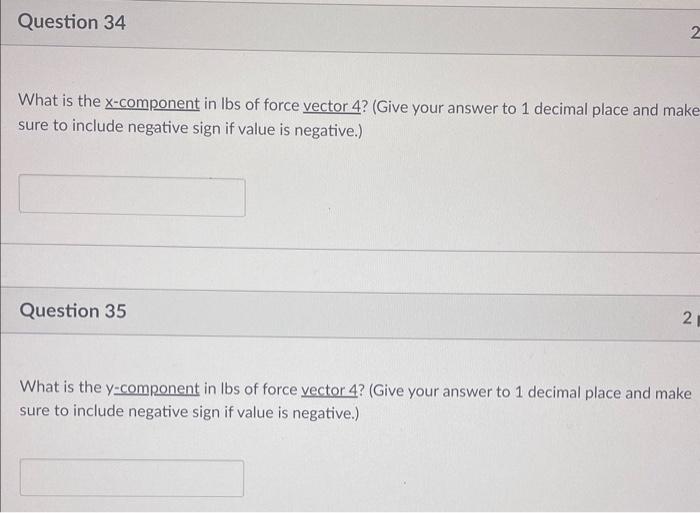(Give your answer to 2 decimal places and make sure to include negative sign if value is negative.) What is the \( \underline{x} \)-component in Ibs of force vector 4 ? (Give your answer to 1 decimal place and make sure to include negative sign if value is negative.) Question 35 What is the \( y \)-component in Ibs of force vector 4? 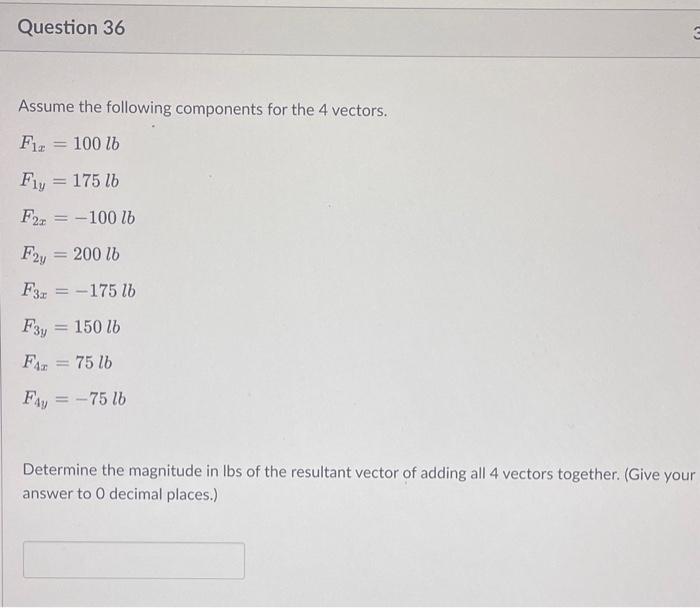(Give your answer to 1 decimal place and make sure to include negative sign if value is negative.) Assume the following components for the 4 vectors. \[ \begin{array}{l} F_{1 x}=100 \mathrm{lb} \\ F_{1 y}=175 \mathrm{lb} \\ F_{2 x}=-100 \mathrm{lb} \\ F_{2 y}=200 \mathrm{lb} \\ F_{3 x}=-175 \mathrm{lb} \\ F_{3 y}=150 \mathrm{lb} \\ F_{4 x}=75 \mathrm{lb} \\ F_{4 y}=-75 \mathrm{lb} \end{array} \] Determine the magnitude in Ibs of the resultant vector of adding all 4 vectors together. 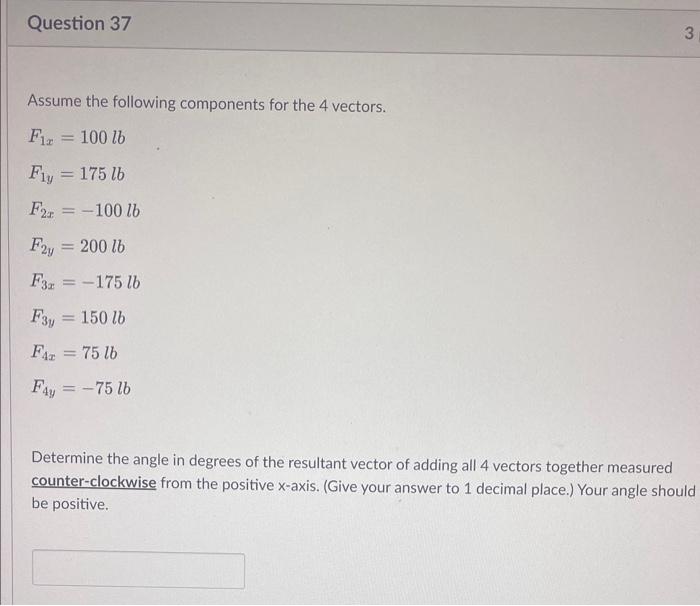(Give your answer to 0 decimal places.) Assume the following components for the 4 vectors. \[ \begin{array}{l} F_{1 x}=100 l b \\ F_{1 y}=175 l b \\ F_{2 x}=-100 l b \\ F_{2 y}=200 l b \\ F_{3 x}=-175 l b \\ F_{3 y}=150 l b \\ F_{4 x}=75 l b \\ F_{4 y}=-75 l b \end{array} \] Determine the angle in degrees of the resultant vector of adding all 4 vectors together measured counter-clockwise from the positive \( x \)-axis. (Give your answer to 1 decimal place.) Your angle should be positive.