(Solved): 1 introduction In this project you will examine disjunctive normal forms for a compound proposition ...

1 introduction In this project you will examine disjunctive normal forms for a compound proposition. Using this form you will generate an arrangement of components on a Logic Gate Simulator that will generate the truth table for your given compound proposition. 2 Disjunctive Normal Forms A compound proposition is said to be in disjunctive normal form (DNF) if it is written as the disjunction of disjuncts where each disjunct consists of a conjunction of atomic formulas or the negation of an atomic formula. For example, \( (p \wedge q) \vee(\neg p \wedge q) \) is a compound proposition in DNF. Every compound proposition can be rewritten into an equivalent DNF. One way to do so is to decompose the truth table into the union (logic OR) of some "unit" logic statements. See problem 1 as an example. Problem 1 (20 points, due 11/1). Can \( Z \) be written into an equivalent DNF in terms of \( \{p, q\} \) that matches the following truth table? Step 1. Construct truth tables for \( (p \wedge q),(\rightarrow p \wedge q),(p \wedge \rightarrow q) \), and \( (\rightarrow p \wedge \rightarrow q) \). What's the pattern? Step 2. The set of the 4 basic compounds (in Step 1) \[ S=\{(p \wedge q),(\rightarrow p \wedge q),(p \wedge \rightarrow q),(\rightarrow p \wedge \rightarrow q)\} \] is called a basis. Using the truth values for \( X \) and \( Y \), identify them with elements in the basis. Step 3. Based on their truth values, write \( Z \) into a logic compound of \( \{X, Y\} \) and further more an cquivalent \( D N F \) in terms of \( \{p, q\} \). 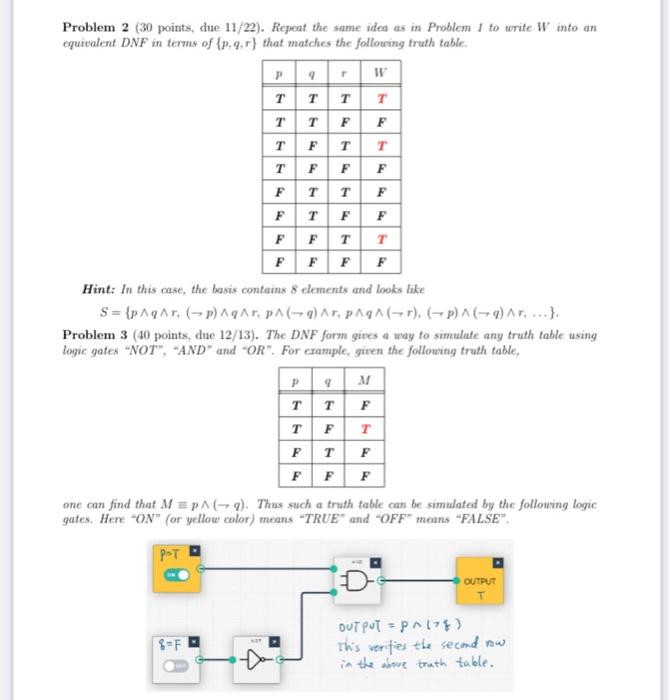Problem 2 ( 30 points, due \( 11 / 22 \) ). Repeat the same ides as in Problem I to write W into an equivalent DNF in terms of \( \{p, q, r\} \) that matches the following fruth table. Hint: In this case, the basis contains 8 elements and looks bike \[ S=\{p \wedge q \wedge r,(\rightarrow p) \wedge q \wedge r, p \wedge(\rightarrow q) \wedge r, p \wedge q \wedge(\rightarrow r),(\rightarrow p) \wedge(\rightarrow q) \wedge r, \ldots\} . \] Problem 3 (40 points, due 12/13). The DNF form gives a way to simulate any truth table using logic gates "NOT", "AND" and "OR". For example, given the following truth table, one can find that \( M \equiv p \wedge(\rightarrow q) \). Thus such a truth table can be simulated by the following logic gates. Here "ON" (or yellow color) means "TRUE" and "OFF" means "FALSE".