(Solved): 1. A hard-bake process is used in conjunction with photolithography in semiconductor manufacturing. ...

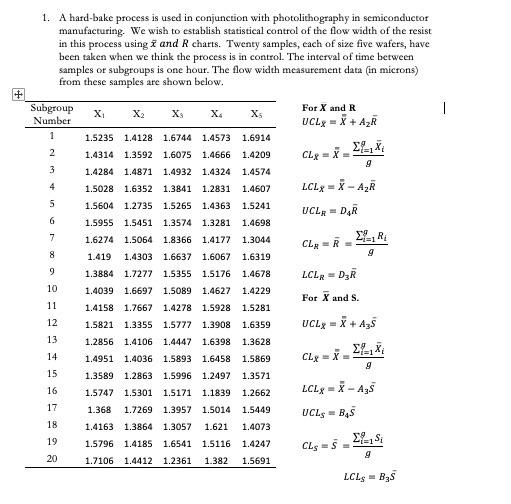
1. A hard-bake process is used in conjunction with photolithography in semiconductor manufacturing. We wish to establish statistical control of the flow width of the resist in this process using \( \tilde{x} \) and \( R \) charts. Twenty samples, each of size five wafers, have been taken when we think the process is in control. The interval of time between samples or subgroups is one hour. The flow width measurement data (in microns) from these samples are shown below. \[ \begin{array}{l} \text { For } X \text { and } \mathbf{R} \\ U C L_{\bar{X}}=\bar{X}+A_{2} \bar{R} \\ C L_{\bar{X}}=\bar{X}=\frac{\sum_{i=1}^{g} \bar{X}_{i}}{g} \\ L C L_{\bar{X}}=\bar{X}-A_{2} \bar{R} \\ U C L_{R}=D_{4} \bar{R} \\ C L_{R}=\bar{R}=\frac{\sum_{i=1}^{g} R_{i}}{g} \\ L C L_{R}=D_{3} \bar{R} \\ \text { For } \bar{X} \text { and } \mathrm{S} . \\ U C L_{\bar{X}}=\bar{X}+A_{3} \bar{S} \\ C L_{\bar{X}}=\overline{\bar{X}}=\frac{\sum_{i=1}^{g} \bar{x}_{i}}{g} \\ L C L_{\bar{X}}=\overline{\bar{X}}-A_{3} \bar{S} \\ U C L_{S}=B_{4} \bar{S} \\ C L_{S}=\bar{S}=\frac{\sum_{i=1}^{g} S_{i}}{g} \\ L C L_{S}=B_{3} \bar{S} \end{array} \] \[ C_{p}=\frac{U S L-L S L}{6 \AA} \] \[ \hat{a}=\frac{\bar{S}}{C_{4}}=\frac{\bar{R}}{d_{2}} \] a) Determine the trial central line and control limits for the \( \bar{X} \) and \( \mathrm{R} \) (18 points). \[ U C L_{X}= \] \[ C L_{X}= \] \[ L C L_{X}= \] \[ U \mathrm{CL}_{R}= \] \[ C L_{B}= \] \[ L C L_{R}= \] b) Determine the trial central line and control limits for the \( \bar{X} \) and \( \mathrm{S} \) (18 points). \[ U C L_{X}= \] \[ C L_{X}= \] \[ L C L_{X}= \] \[ \begin{array}{l} U C L_{S}= \\ C L_{S}= \\ L C L_{S}= \end{array} \] c) If the specifications are at \( 1.50 \pm 0.50 \), what conclusions would you draw about process capability? (15 points) \[ \mathrm{USL}= \] \( \mathrm{LSL}= \) \[ \hat{\sigma}= \] \[ C_{p}= \] Conclusion (circle 1): (a) \( C_{p}>1: \) Process is (b) \( C_{p}=\underline{1} \) : Process is capable (c) \( C_{p}<1 \) : Process is capable of exceeding of meeting specifications incapable of meeting specifications specifications